Binary Search Tree implemented by C++

This is a simple implementation of binary search tree implemented by C++. Here are the methods of my BST:

class Node
{
public:
    Node *left, *right, *parent;
    int key;
};

class BST
{
private:
    Node *nil;

public:
    BST();
    Node* root();

    // Traversals
    void inorder();
    void inorderRec(Node*);
    void inorderIter();
    void preOrder();
    void preOrderRec(Node*);
    void postOrder();
    void postOrderRec(Node*);

    // Search Operations
    Node* find(int);
    Node* minimum(Node*);
    Node* maximum(Node*);
    Node* successor(Node*);
    Node* predecessor(Node*);

    // Element Operation
    void insert(int);
    void insert(Node*);
    void remove(int);
    void remove(Node*);
    void transplant(Node*, Node*);
    bool empty();
};

I will talk about some of the implementations. The complete source file can be found in my algorithm repository. If you found any problem with the implementation, or anything that is worth adding to this, please leave a comment under this article or open an issue in the algorithm repository. This BST does not insert repeated element.

Basic Idea ##

Binary Search Tree is a basic data structure in computer science. It stores data, in my case some integers, into a tree-like structure.

In a tree, there are nodes, which are the storage a piece of data and also connection to other nodes. A node can connect to its parent and its children. In other trees, there could be unlimited children, but for our case, a binary tree could have at most two children. Naturally, let’s call them left and right child respectively.

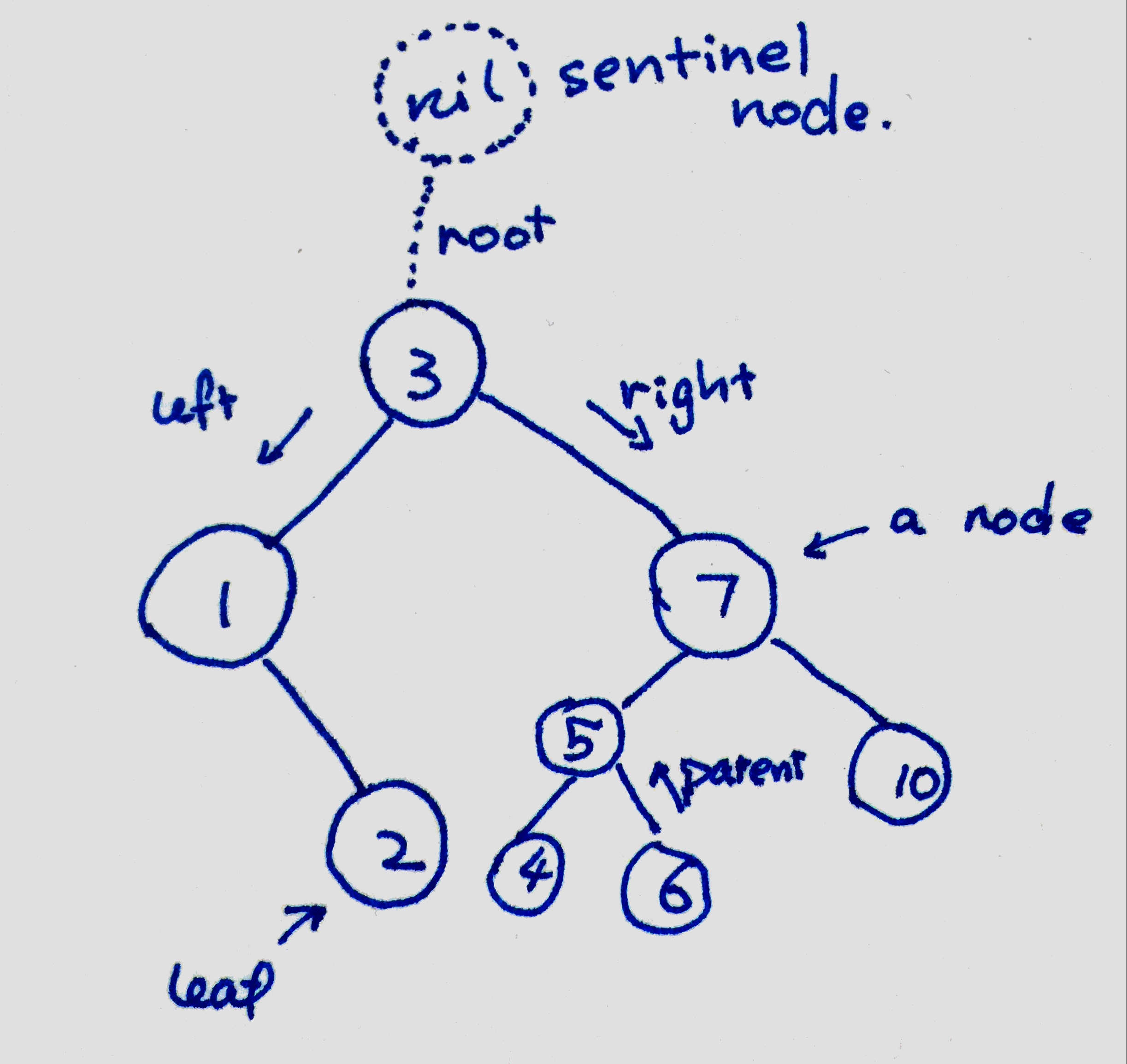
The top node is called root, and the nodes that do not have a child are called leaves. There is a nil sentinel node, which is not in the data structure but a useful element in our program.

Traversals ##

The recursive in-order traversal is easy to implement:

void BST::inorderRec(Node* node)
{
    if (node != nil)
    {
        inorderRec(node -> left);
        cout << node -> key << " ";
        inorderRec(node -> right);
    }
}

The iterative algorithm is slightly more complex. It involves two pointers, marking the current and previous position of our traversal. Although this is not recursive, we could still think of it using an inductive reasoning. We first set the initial states to root and nil (who is the parent of root):

auto x = root();
auto prev = nil;

For an arbitrary iteration, there are three possibilities:

1. prev is the parent of x. It means we have been going downwards in the tree, and both left branch and right branch of x has not yet been explored; then as in-order traversal requires, we go left from here.
2. prev is the left child of x. This means we have just come back from the left branch, implying that the left is already printed. Now we have to print x itself and going to the right.
3. prev is the right child of x. This means we have printed everything in the subtree rooted at x, and should now go up.

The trick here is to 1) progress the printing and 2) ensure that at the end of each iteration, the invariant is preserved, i.e. the situation falls into one of the situations.

prev Pointing at Parent ####

Nothing has been printed, so we go to left directly;

prev = x;
x = x -> left;

We need to consider the case where left is nil, but this is easy because we can just throw prev to left. This works because if we examine the loop invariant, now the tree complies with the second situation.

prev Pointing at left ####

Left tree is already printed (we consider nil as printed), so we try to go right. Don’t forget to first print out x before entering right.

There is a slight complication if x is a leaf, as both children are nil. We would not be able to know whether we have come back from left or right! The traversal will circle around at x forever.

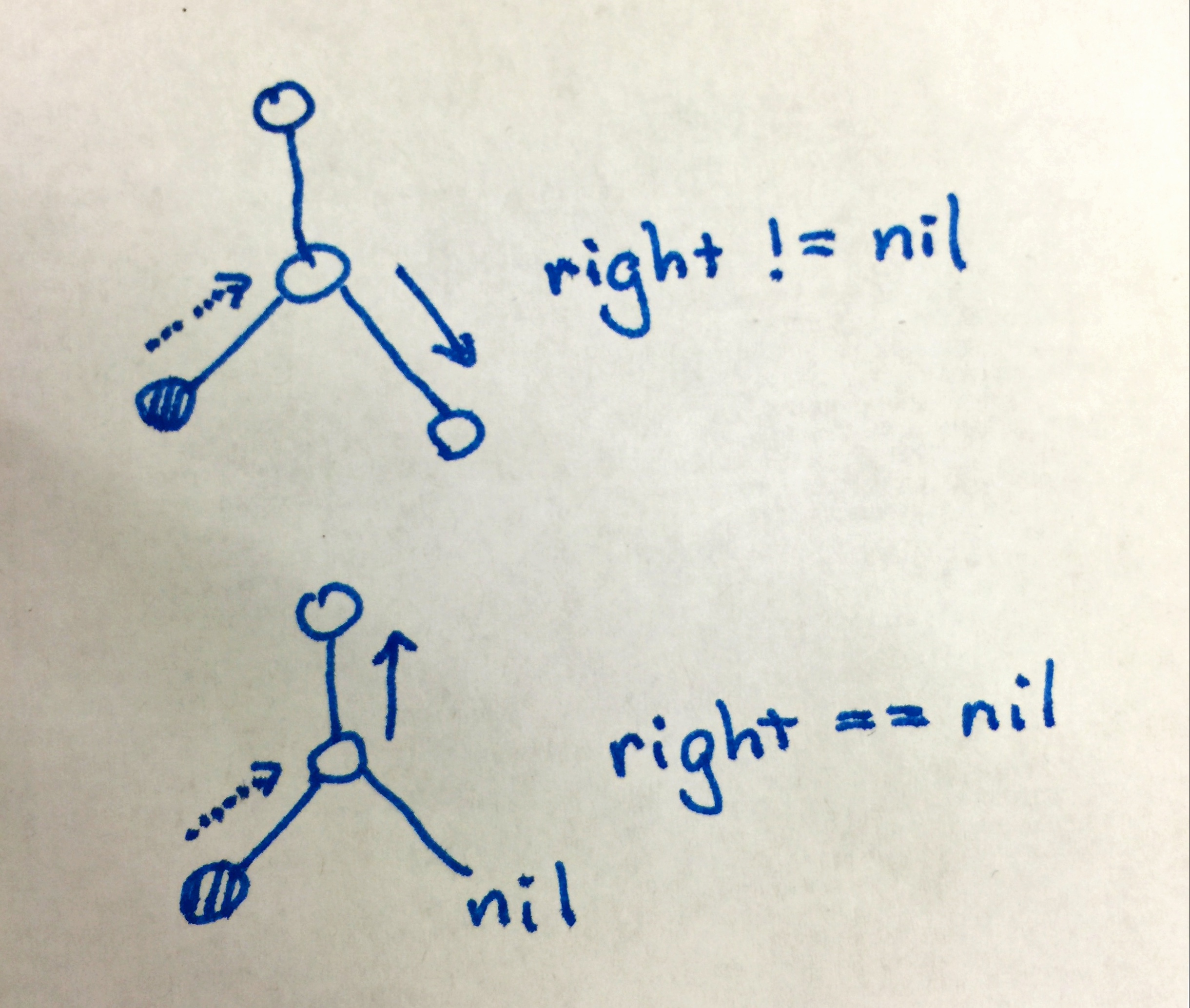{:width=“36px”}.

The solution is that we never come from right at a leaf node. When we reach a leaf node from its left, we directly move upwards.

cout << x -> key << " ";
if (x -> right == nil)
{  // right branch is nil
    prev = x;
    x = x -> parent;
}
else
{
    prev = x;
    x = x -> right;
}

prev Pointing at Right ####

We know x subtree is all printed, so all we need to do is to move x upwards.

prev = x;
x = x -> parent;

Insertion ##

Insertion always occur at leaf in a BST. Generally, we need to 1) find a proper leaf as the parent of our new node and 2) insert it into the proper child of the leaf.

Sentinel Node ##

How is a sentinel node useful? There are several uses of it, and the most important one is to replace NULL for representing a non-existing element. It guards against null pointers.

NULL is a very bad design from the very beginning, as it is passed into a function as pointer type but is not a pointer at all. Any attempt to call a member function will cause a crush. It is also hard to debug, especially when there are layers of function calls. You cannot dereference a null pointer in debugger; it points to 0x00000000, which has no useful information at all.

A sentinel nil on the other hand is a legitimate Node object. It has all functions supported, and could be more useful for debugging. Debugging-wise, it is printable and assignable.

It is also used as the parent of root in our tree. This eliminates the difference between an empty tree and non-empty tree, so insertion and removal of root could be carried out without an extra conditional branch.

Codes ##