Fractals

Fractal #

naming: fractional dimension

Definition: ##

self-similar $$\to$ when zoomed in, look the same

Types: ##

1. Exactly self-similar
2. Statistically self-similar

Exactly Self-similar ##

If zoomed in, there is no way to tell that we have zoomed in.

Sierpinski Carpet ###

• A square divided into 9 squares
• The center square is empty
• Each other square is divided again

Koch Snowflake ###

• Chop the lines into 3 Segments
• replace the middle one with equal lateral triangle
• Chop and replace each segment

The important property is that when we zoom in on an edge, it is arbitrarily “bumpy” - non-smooth. This is similar to things like shorelines. There is a self-similarity in natural shorelines.

However, shorelines are not as bumpy as Koch Snowflakes. They are smoother. Hence, we need a concept to describe the bumpiness.

Length of Koch Snowflake ###

Each Step increases the length to $$\dfrac{4}{3} \times$ original. Hence, Koch Snowflake is infinitely long.

$$l_k = \dfrac{4}{3} l_{k-1}$

Question: How quickly does Koch Snowflake’s length converge to infinity?

Measuring Length of Fractal Line ###

Different measuring scales lead to different length.

From the starting point, jump a fixed distance, $$d_u$, and measure how many $d_u$ are there in the line.

Each different $$d_u$ results in a unique length, and as $d_u$ approaches 0, the length measured approaches $\infty$

The scale is related to length and this function describes the bumpiness of a fractal line. This is called Fractal Dimension.

• Higher Fractal Dimension means more bumpiness
• Lower Fractal Dimension means less bumpiness

Shoreline/Mountain Topology ###

Use fractal dimension to model a bumpy line, and computationally derive the line, rather than describing more details.

Statistically Self-similar ##

Recursive Tree: Tree := Stick + Tree + Tree

Moreover, we need to take care of the angles, length and returning position.

It becomes:

- Stick
- Turn
- Tree  -> this will expand to the same routine
- Turn
- Tree  -> this will expand to the same routine
- Turn
- Backwards

L-System ###

The above process can be described by CFG:

$$T:S\leftarrow T \rightarrow \rightarrow T \leftarrow \overline{S}$

This use of CFG is called L-System.

Improvement to L-System Tree ###

• Randomness : This introduces Statistically similar fractal image.

The sub-parts are statistically similar to the original image, but not exactly the same.

To create a nice tree, it is important to examine each tree. There is a grammar to each type of tree, describing its patterns.

However, sadly trees don’t grow by the fractal model.

Incorporating Randomness Into Fractals ##

Example Algorithm (Subdivide and Offset)

repeat
    foreach segment
        offset midpoint for random distance
        hence create two segments

• deeper repetition: bumpier

More sophisticated examples:

Height Map ###

A raster vector of height

• Can represent any terrain with no overlapping height (not bumpy topology, water, etc.)
• Cannot represent extremely rocky terrain

Diamond Square

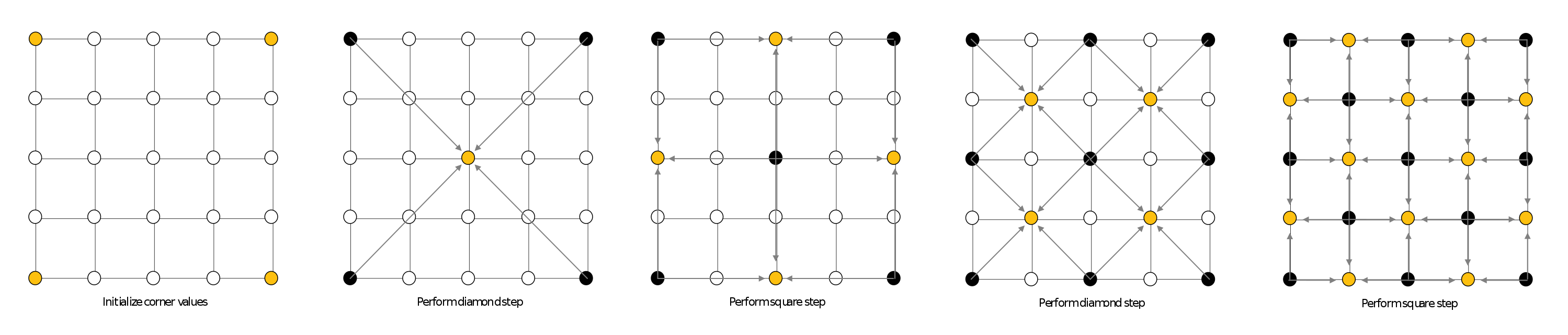
• Level 0: Four corners set to $$h = 0$
• Level 1: Mid-point $$m_1$ set to $h_1 += random$
• Level 2: Point on Edges aligned with $$m_1$, offset randomly
• Level 3: Mid-point of each sub-square, offset randomly
• …

The result could look something like:

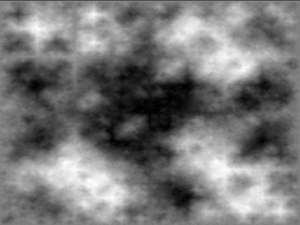
The problem is the grid pattern is visible. There are ‘+’ in the graph, so rotating the graph will be noticed (not entirely natural)

Solution: Use

Applications:

• NOT good for terrain. Natural terrain has very few local minima. The minima will drain, and become global minima. This is not reflected by diamond square subdivision.

• Clouds. Clouds density is similar to the patterns generated from diamond square subdivision.

• Dirt. This could create “dirty” texture to human-created objects.

Perlin Fractal ###

A perlin fractal is created by taking in a height map, downsize it, and fill itself with the small height map.